Trofické funkcie v modeloch dravca a koristi

20 min., 1/3

Pri štúdiu prírody hrajú neoceniteľnú úlohu matematické modely. Tieto modely otvárajú cestu k predpovediam budúceho vývoja, ale plnia aj ďalšie a důležitejšie úlohy.

Používanie ekologických modelov býva niekedy spomínané ako fyzikálne postupy v ekológii, pretože sa študuje ekosystém z hľadiska vývoja populácií a používajú sa na to matematické metódy pôvodne odvodené na riešenie fyzikálnych úloh. Výstupy z modelov potom nesú napríklad nasledujúce informácie.

• Predikcia Schopnosť pracovať s matematickými modelmi ekosystémov umožňuje predpovedať budúci vývoj. Môže sa jednať o vývoj v nemennom prostredí, alebo vývoj v prostredí, v ktorom sa niektorý z parametrov mení. Znalosť modelu potom umožní posúdiť, aký má táto zmena vplyv na ekosystém.
• Porozumenie princípom Matematické modely umožňujú ekológom a vedcom skúmať interakcie medzi rôznymi zložkami ekosystémov a porozumieť dynamike týchto systémov. Pomáhajú tým identifikovať faktory ovplyvňujúce štruktúru a funkciu týchto ekosystémov.
• Optimalizácia rozhodovania Matematické modelovanie ekosystémov môže byť použité na optimalizáciu rozhodovania v oblastiach ako je ochrana biodiverzity alebo manažment lesov a rybolovu. Pomáha identifikovať najlepšie stratégie na dosiahnutie vytýčených cieľov.

Jedným zo základných vzťahov v ekosystémoch je vzťah dravca a koristi. Tento vzťah môže byť jedinou interakciou v ekosystéme alebo môže byť doplnený interakciami ďalšími. Dôležitosť modelovania spolužitia dravca a koristi si objasníme na nasledujúcich historicky významných modeloch.

Lotkov-Volterrov model

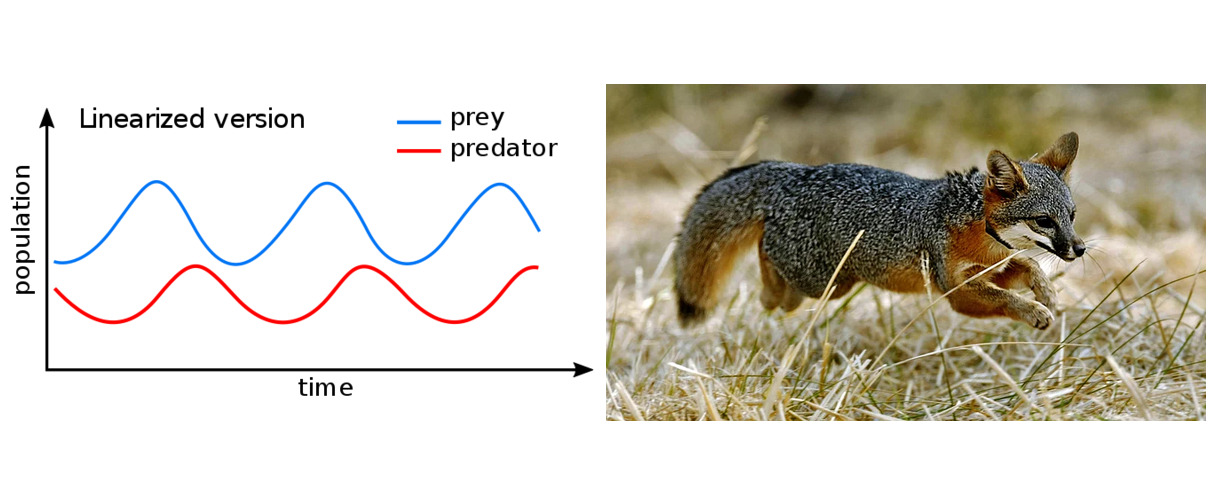
V roku 1926 publikoval jeden z prvých modelov dravca a koristi taliansky matematik Vito Volterra. Motiváciou k zostaveniu tohto modelu bola skutočnosť, že počas obmedzenia rybolovu za prvej svetovej vojny v úlovkoch vzrástlo percento dravých rýb. Na túto skutočnosť upozornil Volterru jeho zať, morský biológ Umberto D’Ancona, ktorý si uvedený jav nedokázal zdôvodniť. Dokonca čakal pravý opak: pri obmedzení rybolovu predpokladal zvýšenie percentuálneho podielu druhov menších rýb, ktoré sú potravou pre dravce. Volterrov model toto správanie vysvetľuje ako dôsledok jednoduchej predstavy interakcie medzi dravými rybami a korisťou.

Model obsahuje dve rovnice. Prvá rovnica popisujúca populáciu koristi obsahuje predpoklad, že táto populácia prirodzene rastie, ale rast je spomalený pôsobením dravcov. Viac dravcov vedie k väčšiemu spomaleniu rastu koristi. Príliš veľa dravcov môže viesť dokonca k tomu, že veľkosť populácie koristi bude klesať a korisť vymrie. Rovnica venovaná populácii dravcov obsahuje predpoklad, že bez prítomnosti koristi populácia dravca vymiera. Čím viac koristi ale majú dravce k dispozícii, tým skôr sa toto vymieranie obráti v nárast populácie dravca.

V systéme popísanom vyššie vznikajú prirodzene cykly. Dostatok koristi umožní nárast populácie dravcov. Mnoho dravcov potom pôsobí na populáciu koristi negatívne do tej miery, že populácia koristi začne vymierať. Toto vymieranie má za následok nedostatok potravy pre dravce a tí začnú tiež vymierať. Po čase je populácia dravca redukovaná natoľko, že korisť prítomnosť dravca pociťuje málo. Preto môže jej populácia zase rásť a namnožiť sa do pôvodného stavu. To však opäť umožní rast populácie dravca a uzatvára sa cyklus. Veľmi pekne sú periodické zmeny veľkosti oboch populácií zreteľné zo záznamov výkupu kožušín snehovej zajaca a rysa v oblasti Hudsonovho zálivu.

Volterra svojim modelom vysvetlil nielen vznik cyklov, ale aj to, že obmedzením lovu sa rovnovážna poloha, okolo ktorej populácie dravca a koristi oscilujú, posunie v prospech dravca a nie koristi. Tento jav, ktorého si všimol D’Ancona, sa nazýva Volterrov efekt.

Rovnaký model ako Volterra navrhol už v roku 1910 americký matematik Alfred J. Lotka, a preto sa model dnes nazýva Lotkov-Volterrov model.

Model bukač smrekový

Podobné periodické výkyvy ako v Lotkovom-Volterrovom modeli je možné pozorovať aj v kanadských lesoch. Tu približne po 30 až 40 rokoch dochádzalo k masovému premnoženiu bukača smrekového (Choristoneura fumiferana). Populácia tohto motýľa je relatívne malá, ale niektoré roky sa zvýši tisícnásobne a jeho húsenice dokážu zahubiť až 80% stromov v lese a ten tak prakticky zničiť. Jeden z posledných masových výskytov bol od roku 2006 v Quebecu. Tu bolo do roku 2019 zasiahnutých cca 9,6 milióna hektárov lesa ¹, čo je viac ako rozloha Maďarska.

V roku 1978 navrhli vedci D. Ludwig, D. D. Jones a C. S. Holling model, ktorý dokázal nielen modelovať vývoj populácie bukača, ale pomohol objasniť aj dôvody, prečo k popisovanému premnoženiu dochádza. Dôvodom bola predácia. V tomto prípade išlo o konzumáciu húseníc bukača vtákmi. Vtáky slúžili v prírode ako faktor obmedzujúci počty húseníc, avšak len do istého limitu. Keď sa les dostatočne rozrástol, poskytol dostatok potravy aj populácii húseníc. Populácia húseníc sa potom rozrástla do takej miery, že vtáky dosiahli pri konzumácii potravy svoju saturáciu a nedokázali ďalej stavy húseníc redukovať. Tým sa úloha vtákov ako predátorov stala menej významnou a populácia húseníc sa mohla veľmi rýchlo množiť a potom zdevastovať les.

V tomto prípade je predácia dôležitá pre obmedzenie populácie húseníc. Pretože vtáky ako predátori majú oveľa pomalší cyklus rozmnožovania než bukač, je možné ich populáciu považovať za konštantnú. Vďaka saturácii potom vtáky dokážu obmedziť rýchlosť rastu bukača len do obmedzenej miery. Toto obmedzenie však od určitej veľkosti populácie bukača prestáva stačiť a dôjde k jeho nekontrolovateľnému premnoženiu.

Model líšky ostrovnej

Líška ostrovná (Urocyon littoralis) je jedinečný živočíšny druh, endemit žijúci len na ostrovčekoch okolo Kalifornie. Je veľká ako mačka a vďaka absencii prirodzených nepriateľov dôverčivá. Ako druh je citlivá a zraniteľná vplyvom malej genetickej variability a malej odolnosti voči chorobám zavlečeným z pevniny. Je to jedna z najmenších psovitých šeliem. Na rozdiel od ostatných psovitých šeliem ale vie šplhať po stromoch.

Vplyvom činnosti človeka sa populácia líšky ostrovnej dostala na prelome tisícročí do veľkých ťažkostí. Na ostrove San Miguel klesla populácia z 450 dospelých jedincov v roku 1994 na 15 v roku 1999 ². Podobná situácia bola aj na okolných ostrovoch, z ktorých každý je osídlený samostatným poddruhom líšky ostrovnej. Príčinou úhynu bol celý reťazec udalostí: produkcia insekticídu DDT v 40. rokoch 20. storočia mala za následok vymretie orla bielohlavého (Haliaeetus leucocephalus) a ten bol nahradený orlom skalným (Aquila chrysaetos). Predátora živiaceho sa rybami týmto na ostrove vystriedal predátor preferujúci cicavce. Toto bolo pre líšky ostrovné fatálne. Líšky, predtým vrcholní predátori, sa zrazu stali korisťou a na prelome tisícročí sa ocitli tesne pred vyhubením. A na rozdiel od Lotkovho–Volterrovho modelu nebolo možné dúfať v návrat líšok na pôvodné stavy vďaka osciláciám, pretože orly mali aj alternatívnu potravu v podobe divokých ošípaných a skunkov.

Našťastie sa nesmiernym úsilím podarilo líšky ostrovné ako druh zachrániť. Najprv sa podarilo správne identifikovať príčiny ich úbytku. Potom už stačilo populáciu líšok opätovne rozmnožiť a zabezpečiť podmienky, v ktorých je populácia stabilná. To zahrňovalo vybíjanie divokých ošípaných, presídlenie orlov skalných, návrat orlov bielohlavých, umelé rozmnoženie líšok, ich návrat do prírody a ich vakcináciu proti zavlečeným chorobám. To všetko sa podarilo v rekordnom čase, za jednu dekádu. Jednalo sa o jeden z najúspešnejších záchranných programov pre cicavce.

Trofické funkcie

Dôležitou komponentou modelov dravca a koristi, či ide o ktorýkoľvek z vyššie uvedených prípadov, je trofická funkcia. Táto funkcia modeluje pôsobenie jedného predátora na populáciu koristi. Udáva rýchlosť, s akou spomaľuje rast koristi jeden dravec. Je-li \(x\) veľkosť populácie koristi a \(y\) rýchlosť, s akou jeden dravec spomaľuje rast koristi (t. j. množstvo koristi ulovenej dravcom za jednotku času), môžeme túto funkciu matematicky zapísať v tvare \[y=f(x).\] Budeme sa snažiť nájsť prirodzené predpoklady, ktoré trofická funkcia musí spĺňať. Potom sa pre ňu pokúsime nájsť vhodný analytický tvar.

Riešenie.

1. Funkcia \(y=f(x)\) je rastúca.

2. Funkcia \(y=f(x)\) prechádza počiatkom, t. j. platí \(f(0)=0\).

3. Funkcia \(y=f(x)\) je zhora ohraničená. Keďže je funkcia rastúca a zhora ohraničená, tak má jej graf vodorovnú asymptotu v nekonečne.

Trofická funkcia Hollingova typu II

Trofická funkcia udáva, koľko koristi zahubí jeden dravec za jednotku času pri danej veľkosti populácie koristi. Musí teda byť definovaná na množine nezáporných čísel a funkčné hodnoty budú nezáporné (toto plynie aj z bodov 1 a 2 v predchádzajúcej úlohe). V predchádzajúcej časti bolo ukázané, že trofická funkcia má prechádzať počiatkom a rásť k vodorovnej asymptote (rast a ohraničenosť zhora). Tieto vlastnosti nebudú splnené, ak budeme hľadať trofickú funkciu medzi lineárnymi funkciami. Skúsime teda najjednoduchšiu nelineárnu funkciu, nepriamu úmernosť.

Riešenie. Funkcia, ktorej graf vznikne preškálovaním grafu funkcie \(y=\frac{1}{x}\) vo zvislom smere \(k\)-krát je \[y=\frac{k}{x}.\] Prevrátenie dosiahneme vynásobením funkcie faktorom \(-1\) a posunu dosiahneme pripočítaním hodnoty \(S\). Týmito úpravami dostávame funkciu \[y=S-\frac{k}{x}.\] Posun doľava o \(b\) zabezpečíme substitúciou výrazu \(x+b\) za \(x\). Tým dostávame funkciu \[y=S-\frac {k}{x+b}.\] Po prevedení na spoločného menovateľa má funkcia tvar \[y=\frac{Sx+Sb}{x+b}-\frac{k}{x+b}=\frac{Sx + (Sb-k)}{x+b}.\] Má-li platiť \(f(0)=0,\) musí byť splnená podmienka \[Sb-k=0.\] Táto podmienka ukazuje, že tri konštanty nie sú nezávislé, ale je medzi nimi uvedená väzba.

Poznámka. V predchádzajúcej úlohe sme odvodili analytický tvar pre jednu zo základných trofických funkcií. Jedná sa o rastúcu funkciu, ktorá zo začiatku rastie smerom k vodorovnej asymptote a rýchlosť rastu postupne klesá. Taká funkcia sa nazýva Hollingova funkcia II typu. Býva obvyklé ju písať v tvare \[f(x)=\frac {Sx}{x+b},\tag{1}\] kde \(S\) je hladina saturácie a \(b\) konštanta, ktorej význam objasníme v nasledujúcej úlohe.

Riešenie. Priamym dosadením do (1) dostávame \[f(b)=\frac{Sb}{b+b}=\frac {Sb}{2b}=\frac S2.\] Tým je tvrdenie dokázané.

Nasledujúca úloha ukazuje opačný proces, keď z trofickej funkcie v tvare (1) odvodíme tvar ukazujúci postupné transformácie funkcie \(y=\frac 1x\).

Riešenie. Úlohu vyriešime tak, že zlomok šikovne upravíme. V čitateli vytvoríme násobok menovateľa, zlomok rozdelíme na dva a skrátime:

\[\frac {6x}{x+2} = \frac {6(x+2)-12}{x+2}=\frac {6(x+2)}{x+2}-\frac {12}{x+2}=6-12\frac 1{x+2}\]

Tento výpočet ukazuje, že graf uvedenej funkcie obdržíme rozšírením grafu funkcie vo zvislom smere dvanásťkrát, prevrátením okolo vodorovnej osi, posunutím o šesť jednotiek nahor a dve jednotky doľava.

Rovnakého výsledku by sme dosiahli aj tak, že by sme menovateľa vydelili čitateľom.

Riešenie. Vďaka poznámke pred treťou úlohou o všeobecnom tvare trofickej funkcie vieme, že predpis bude tvaru \[ y=\frac{Sx}{x+b}, \] kde \(S\) je hodnota saturácie predátora, t. j. \[ y=\frac{6x}{x+b}\,. \] Hodnotu parametra \(b\) môžeme rovno povedať vďaka Úlohe 3, ale môžeme ju tiež rýchlo dopočítať z druhej podmienky zo zadania, keďže vieme, že \[ 3=\frac{6\cdot 210}{210+b} \] a odtiaľ plynie \(b=210\). Predpis výslednej funkcie je teda \[ y=\frac{6x}{x+210}. \]

Literatúra a odkazy

Literatúra

• Wikipedia, https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations March 3, 2024
• R Mařík, Dynamické modely populací, https://robert-marik.github.io/dmp/uvod.html, March 3, 2024
• D. Ludwig, D.D. Jones, C.S. Holling: Qualitative analysis of insect outbreak systems: the spruce budworm and forest, Journal of Animal Ecology 47(1): 315–332, February 1978.

Zdroje obrázkov

• https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations#/media/File:Lotka_Volterra_dynamics.svg
• https://www.npr.org/sections/thetwo-way/2016/08/11/489695842/once-nearly-extinct-california-island-foxes-no-longer-endangered Kevork Djansezian/AP