Krvný tlak

45 min., 2/3

Goniometrické funkcie a periodické javy

Základné goniometrické funkcie sínus a kosínus sa často používajú na modelovanie svetelných, zvukových a elektromagnetických vĺn. Dajú sa použiť aj na aproximáciu ¹ ďalších periodických javov, ako sú napríklad príliv a odliv alebo krvný tlak. Pochopenie týchto funkcií (a ich jednotlivých častí) nám umožňuje efektívne predpovedať a analyzovať periodické javy a ich vlastnosti. Môžeme napríklad vypočítať výšku morských vĺn alebo čas prílivu. V nasledujúcom texte sa zameriame na funkcie, ktoré aproximujú krvný tlak.

Základné informácie o krvnom tlaku

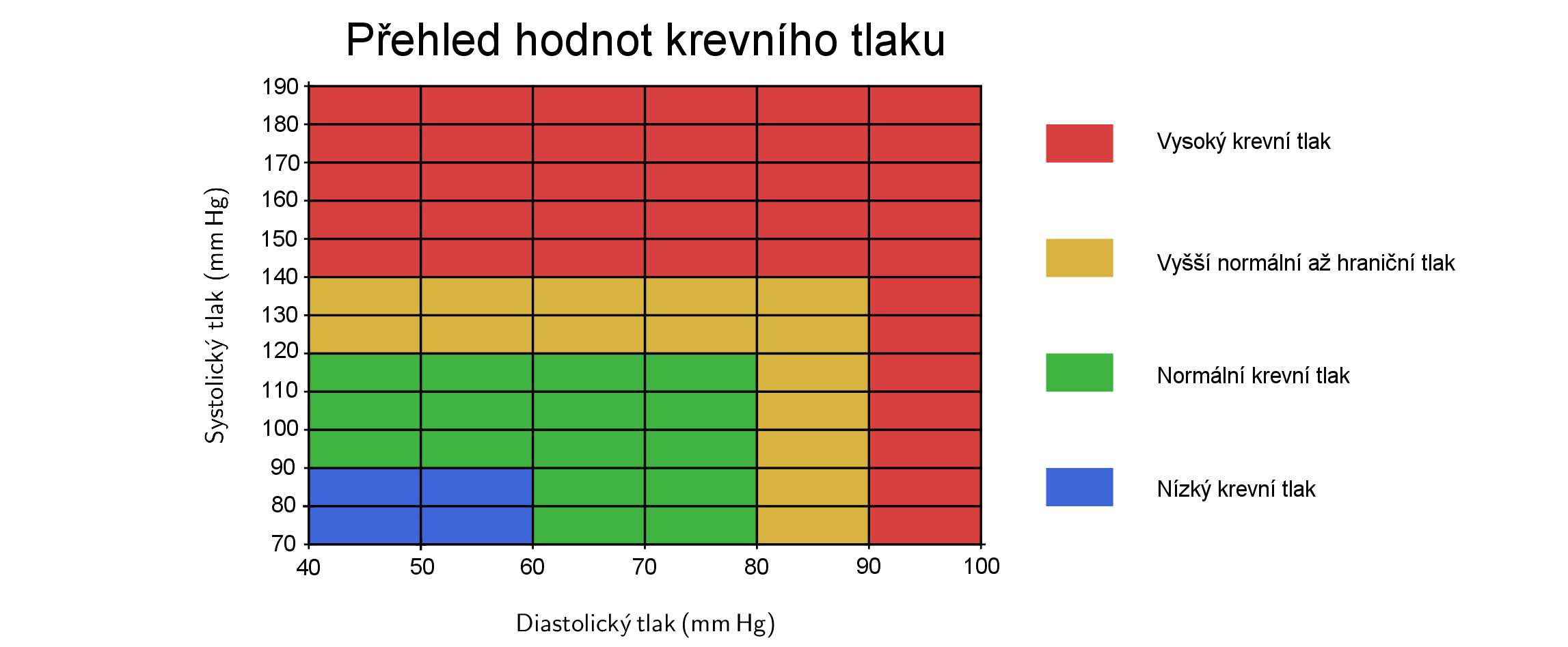
Srdce funguje ako pumpa, ktorá poháňa okysličenú krv do ciev celého tela, aby mu dodala potrebný kyslík a živiny. Krvný tlak je tlak, ktorým pôsobí krv na stenu cievy, cez ktorú preteká. Tento tlak je rôzny v rôznych častiach krvného obehu. Bežne sa krvný tlak chápe ako arteriálny (tepnový) tlak, teda tlak krvi vo veľkých tepnách. Ak je váš krvný tlak príliš vysoký, zaťažuje vaše tepny (a srdce), čo môže viesť k srdcovému infarktu alebo mozgovej príhode. Vysoký krvný tlak, odborne hypertenzia, sa zvyčajne nijako nepociťuje ani nepozoruje. Nemá tendenciu spôsobovať zjavné príznaky či symptómy. Jediný spôsob, ako zistiť hodnotu krvného tlaku, je nechať si ho zmerať. Prvé meracie prístroje určovali krvný tlak podľa výšky stĺpca ortuti, preto sa jeho hodnota dodnes uvádza v milimetroch ortuti. Zapisuje sa ako pomer dvoch čísel. Ak je vaša hodnota napríklad \(120/80\,\text{mm}\,Hg\), krvný tlak sa číta ako \(120\) na \(80\).

Vyššie číslo udáva systolický krvný tlak. Jedná sa o najvyššiu hodnotu, ktorú tlak dosiahne, keď srdce bije a vytláča krv do ciev. Nižšie číslo je diastolický krvný tlak a je to naopak najnižšia úroveň tlaku v okamihu, keď sa srdcový sval medzi údermi uvoľňuje. Nižšie uvedená tabuľka zobrazuje rozmedzie nízkeho, normálneho a vysokého krvného tlaku.

Aproximácia funkcie krvného tlaku

Pri sťahoch srdca sa krvný tlak cyklicky zvyšuje a znižuje. Dĺžka trvania jedného srdcového tepu teda zodpovedá perióde funkcie, ktorá opisuje krvný tlak. Každá perióda funkcie merania krvného tlaku teda zodpovedá jednému srdcovému tepu (udáva, ako dlho trvá, kým sa dokončí cyklus srdcového tepu) Lokálne maximum funkcie predstavuje systolický tlak a lokálne minimum diastolický tlak. Funkciu krvného tlaku môžeme približne nahradiť sínusovou alebo kosínusovou funkciou.

Všeobecný tvar funkcie sínus je \[ f\left(x\right) = a\cdot\sin\left(bx + c\right) +d, \]

kde \(a\) je amplitúda, ktorá určuje, ako vysoko alebo nízko sa sínusoida pohybuje od svojej strednej hodnoty. Hodnota \(b\) ovplyvňuje periódu funkcie (platí, že perióda je rovná \(\frac{2\pi}{|b|}\).). Člen \(c\) určuje posun v smere osy \(x\) a \(d\) posun ve směru osy \(y\).

Riešenie. Periódu \(p_1\) funkcie \(P_1\) môžeme vypočítať ako \[p_1=\frac{2\pi}{\frac{7\pi}{3}}=\frac{6}{7}\,\text{sekundy}.\] Keďže doba trvania jedného srdečného tepu je \(\frac{6}{7}\) sekundy, tepová frekvencia \(f_1\) bude \[ f_1=\frac{60}{\frac{6}{7}}=70\,\text{úderov za minútu}. \]
Rovnako pre funkciu \(P_2\) bude perióda \[ p_2=\frac{2\pi}{2\pi}=1\,\text{sekunda}. \] Tepová frekvencia je teda \(f_2=60\) úderov za minutu.

Riešenie. Na vykreslenie grafu funkcie bude os \(x\) predstavovať čas \(t\) v sekundách. Os \(y\) bude predstavovať krvný tlak \(P\) v milimetroch ortuti. Jednotky na osiach zvolíme tak, aby graf vyzeral prehľadne. Vhodná voľba je napríklad taká, že jednej jednotke na osi \(x\) zodpovedá sto jednotiek na osi \(y\). V riešení na obrázku je zvolený pomer jednotiek na osiach \(1:125\). Funkcia \[ P_1=25\cdot\sin\left(\frac{7\pi}{3}t\right)+105 \] osciluje okolo hodnoty \(105\), amplitúda je rovná \(25\). Lokálne maximá funkcie budú mať teda funkčnú hodnotu \(105+25=130\) (systolický tlak). Lokálne minimá funkcie budú mať funkčnú hodnotu \(105-25=80\) (diastolický tlak).

Funkcia \[ P_2=30\cdot\cos\left(2\pi t\right)+125 \] osciluje okolo hodnoty \(105\), amplitúda je rovná \(30\). Lokálne maximá funkcie budú mať teda funkčnú hodnotu \(125+30=155\) (systolický tlak). Lokálne minimá funkcie budú mať funkčnú hodnotu \(125-30=95\) (diastolický tlak).

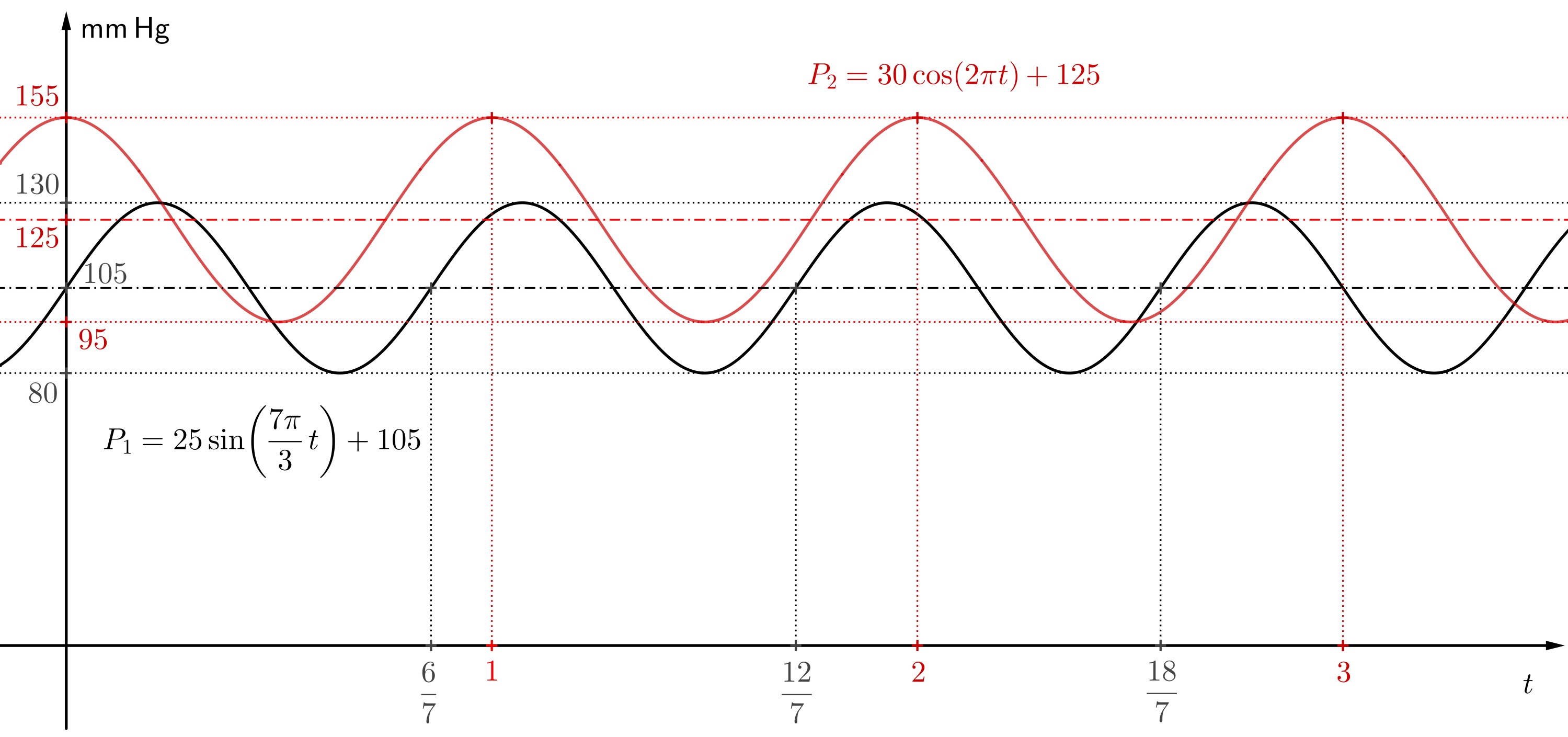
Funkcia \(P_1\) je približne funkciou tlaku \(130\) na \(80\), podľa tabuľky z úvodu zodpovedá hodnotám medzi normálnym a vysokým tlakom (v niektorých krajinách sa považuje za normálny tlak, v niektorých krajinách je to už spodná hranica vysokého krvného tlaku). Funkcia \(P_2\) zodpovedá tlaku \(155\) na \(95\), tento tlak je vysoký.

Vizualizácia takýchto grafov pomáha porozumieť zmenám krvného tlaku a pochopiť ďalšie periodické javy, čo je nevyhnutné ako v matematických štúdiách, tak v praktických aplikáciách.

Vysoký krvný tlak je nebezpečný stav a hlavný rizikový faktor srdcových ochorení a mŕtvice. Zdravý životný štýl, napríklad strava s vysokým obsahom ovocia a zeleniny a nízkym obsahom sodíka, ako aj fyzická aktivita, môže pomôcť predchádzať vysokému krvnému tlaku. Vysoká hodnota z jediného merania nemusí nutne znamenať, že máte vysoký krvný tlak, pretože na krvný tlak môže počas dňa pôsobiť mnoho faktorov, napríklad teplota, doba posledného jedla alebo stres. Vďaka tomu, že sme si funkcie \(P_1\) a \(P_2\) vykreslili, vidíme na prvý pohľad, aké sú medzi nimi rozdiely. Niekedy však môžu mať dve funkcie dané na prvý pohľad rôznymi predpismi ten istý graf. Spoznali by ste napríklad na prvý pohľad, že tomu tak je u nasledujúcich dvoch funkcií?

\[ y=\sin\frac{3x}{5},\qquad y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right) \] Tieto funkcie majú rovnaký graf a veľkosť ich periódy je \[ \frac{2\pi}{\frac{3}{5}}=\frac{10\pi}{3}. \]

Ale pozor, graf funkcie \(y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right)\) nie je oproti grafu funkcie \(y=\cos\frac{3x}{5}\) posunutý v smere osi \(x\) o \(\frac{\pi}{2}\), ako by sa z predpisu funkcie na prvý pohľad mohlo zdať, ale o štvrtinu periódy tejto funkcie. To môžeme vidieť, ak si predpis vhodne upravíme: \[ y=\cos\left(\frac{3x}{5}-\frac{\pi}{2}\right)=\cos\left(\frac{3}{5}\left(x-\frac{5\pi}{6}\right)\right) \]

Na porovnanie dvoch takýchto funkcií by teda bolo lepšie, keby sme mohli jednu previesť na druhú. Týmto sa práve bude zaoberať nasledujúca úloha.

Riešenie. Pre funkcie \(\sin x\) a \(\cos x\) v základnom tvare platí \[ \sin x=\cos\left(x-\frac{\pi}{2}\right), \] kde \(\frac{\pi}{2}\) je štvrtina periódy. Perióda funkcie \(P_1\) je \(p_1=\frac{6}{7}\), štvrtina periódy je \[ \frac{p_1}{4}=\frac{6}{28}=\frac{3}{14}. \] Platí teda \[ \sin\left(\frac{7\pi}{3}t\right)=\cos\left(\frac{7\pi}{3}\left(t-\frac{3}{14}\right)\right) \] a funkciu \(P_1\) môžeme vyjadriť nasledovne \[ P_1=25\cdot\cos\left(\frac{7\pi}{3}t-\frac{1}{2}\pi\right)+105. \]

V predchádzajúcej úlohe by sme mohli funkcie tiež zameniť a vyjadrovať funkciu \(P_2\) pomocou funkcie sínus.

Riešenie. Na aproximáciu funkcie krvného tlaku použijeme napríklad funkciu sínus (riešenie pre funkciu kosínus by bylo obdobné).

Amplitúda funkcie je \(\frac{110-70}{2}=20\) a funkcia osciluje okolo hodnoty \(\frac{110+70}{2}=90\).

Perióda funkcie je \[ p=\frac{60}{50}=\frac{6}{5}, \] t. j. jeden srdcový tep trvá \(1{,}2\) sekundy. Zo vzťahu \[ p=\frac{2\pi}{b} = 1{,}2 \] pre periódu \(p\) funkcie dostávame \(b= \frac{5}{3}\pi\).

Hodnotu \(c\) môžeme zvoliť ľubovoľne, najjednoduchšie je zvoliť \(c = 0.\) Dosadením vyššie uvedených hodnôt do všeobecného tvaru funkcie dostávame \[ P(t) = 20\cdot\sin\left(\frac{5\pi}{3}t\right)+90. \]

Táto funkcia približne modeluje krvný tlak osoby so zadanými hodnotami ako funkciu času (v sekundách).

Auskultačná technika merania krvného tlaku

Na záver ešte uveďme, ako sa v realite tlak naozaj meria. Jedna z presných metód je tzv. auskultačná technika. Pri tejto metóde sa používa tonometer, pozostávajúci z gumovej manžety, nafukovacieho vaku a manometra (mechanické meradlo tlaku), a fonendoskop.

Gumová manžeta tonometra sa nasadí približne na polovicu ramena. Tlak v manžete sa zvýši tak, aby prevyšoval tlak v tepne. Tým sa z manžety stane umelo vytvorená prekážka krvnému prietoku. Postupným pomalým znižovaním tlaku v manžete dôjde v určitom okamihu k obnoveniu prietoku krvi.

Tlak v manžete však na začiatku spôsobí deformáciu tepny, vďaka ktorej je prúdenie prenikajúcej krvi turbulentné. Hodnota tlaku, pri ktorej začínajú byť vo fonendoskope počuteľné srdcové ozveny, zodpovedá hodnote systolického krvného tlaku.

Ozveny sú počuteľné dovtedy, kým tlak v manžete postačuje na deformáciu tepny a tým na udržanie turbulentného prúdenia. Hneď ako tlak v manžete poklesne natoľko, že už nestačí tepnu deformovať, obnoví sa pôvodné prúdenie krvi a ozveny prestanú byť počuteľné. Tlak pri poslednej počuteľnej ozvene zodpovedá hodnote diastolického krvného tlaku.

Spresňovanie

Zostáva dodať, že realistickejšie vyjadrenie funkcie krvného tlaku je náročnejšie a vyžaduje súčty goniometrických funkcií s rôznymi periódami.

Na nasledujúcom obrázku vidíme konkrétny príklad takéhoto súčtu a príslušný graf. Súčasne je na obrázku znázornené meranie krvného tlaku. Rýchlosť vypúšťania manžety je približne konštantná. Tlak v manžete teda klesá konštantnou rýchlosťou (opäť približne) a na obrázku je znázornený priamkou.

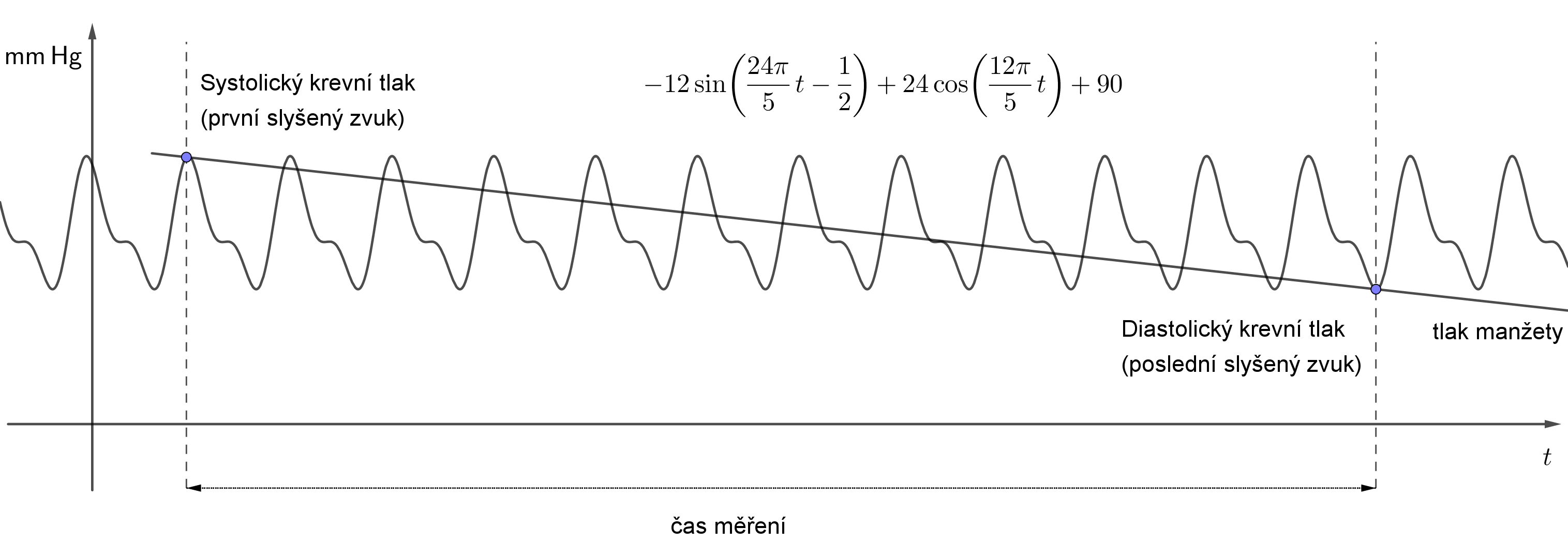
Spresňovanie priebehu funkcie krvného tlaku pomocou súčtov sínusov a kosínusov už súvisí s tzv. Fourierovou vetou, ktorá hovorí, že spojitú periodickú funkciu možno vyjadriť ako súčet nekonečného počtu funkcií sínus a kosínus, pričom každý z týchto členov má určitú amplitúdu a periódu.

Tento výsledok získal v roku 1822 francúzsky matematik Joseph Fourier ako súčasť riešenia rovnice vedenia tepla. Jedná sa o kľúčový koncept pre analýzu a pochopenie akýchkoľvek periodických javov. Fourierova veta je základom spracovania signálov.

Literatúra

• https://www.vaia.com/en-us/textbooks/math/calculus-an-applied-approach-8-edition/chapter-8/problem-72-health-the-function-p100-20-cos-5-pi-t-3-approxim/
• https://www.vaia.com/en-us/textbooks/math/precalculus-9-edition/chapter-4/problem-90-the-function-p100-20-cos-frac5-pi-t3-approximates/#short-answer
• https://www.bloodpressureuk.org/your-blood-pressure/understanding-your-blood-pressure/what-do-the-numbers-mean/