Akustický tomograf a rovnica elipsy

15 min., 1/3

Predstavte si, že potrebujete posúdiť zdravotný stav starého stromu, ani by ste ho museli poraziť alebo doň rezať. Moderné technológie dnes umožňujú takéto posúdenie vykonať šetrne a pritom presne – a jedným z kľúčových nástrojov je pritom rovnica elipsy. Pomocou metódy EBSI (elliptise-based spatial interpolation) možno z nameraných údajov odhadnúť fyzikálne vlastnosti dreva vnútri kmeňa a získať tak predstavu o jeho pevnosti a zdraví. K tomu je však potrebné vedieť zaobchádzať s rovnicou elipsy aj vtedy, keď je elipsa vo všeobecnej polohe vzhľadom k osiam. V takom prípade využijeme skalárny súčin pre nájdenie projekcie vektora do požadovaného smeru.

Akustický tomograf

V praxi arboristu, odborníka pre starostlivosť o dreviny mimo lesa, je častou úlohou posúdenie vitality a zdravotného stavu stromu. Toto je nutné urobiť s nulovým alebo minimálnym zásahom, ktorý kondíciu stromu výrazne neovplyvní. Jednou z veľmi málo invazívnych metód je použitie akustického tomografu. Jedná sa o prístroj, ktorý dokáže merať “dobu letu” zvukového signálu (anglicky používaný termín time of flight, TOF) medzi dvoma senzormi. S pomocou metód analytickej geometrie je potom možné určiť vzdialenosť medzi senzormi a s využitím predpokladu o šírení zvukových signálov priamymi lúčmi sa dá zistiť rýchlosť šírenia zvuku v materiáli. Táto hodnota je veľmi dôležitým indikátorom fyzikálno-mechanických vlastností, pretože v zdravom dreve (angl. sound wood) sa zvuk šíri rýchlejšie ako v dreve degradovanom (angl. degraded wood).

Problematika rekonštrukcie obrazu

Rekonštrukcia obrazu v akustickom tomografe vychádza z predpokladu priameho šírenia lúčov v reze kmeňa. Nie sú teda brané do úvahy odrazy alebo lom vlnenia. Kvalita tohto predpokladu je predmetom aktuálneho vedeckého skúmania, avšak predpoklad tohto typu je nutné pre praktické využitie metódy urobiť.

Pretože sa vychádza z pomerne malého množstva lúčov (akustický tomograf má typicky 12, najviac 24 senzorov, pre stromy malého priemeru aj menej), je nutné využiť nejakú metódu interpolácie a spriemerovávania. Týmto sa úloha stáva odlišnou napríklad od tomografov používaných v zdravotníctve, kde zobrazovacích lúčov je rádovo viac a je tiež lepšie definovaná geometria merania: zdroje a snímače sú umiestnené napríklad po obvode kruhu a nie po nepravidelnom obvode kmeňa stromu. Pre odstránenie nedostatkov spojených s použitím akustického tomografu pre stromy bolo vyvinutých niekoľko techník, ktoré umožňujú interpoláciu a spriemerovávania nameraných hodnôt.

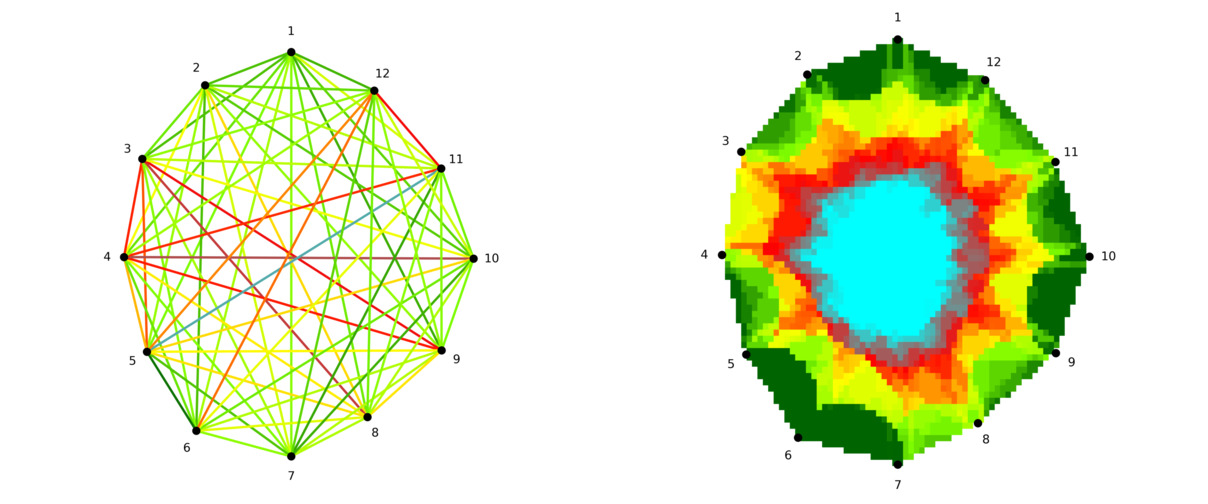
EBSI metóda a jej nástupcovia

Rad metód rekonštrukcie obrazu v akustickom tomografe vychádza z predpokladu, že rýchlosť šírenia zvuku je ovplyvnená kvalitou dreva v eliptickom okolí spojnice dvoch senzorov. Tento predpoklad bol otestovaný na reálnych meraniach v Du et al. (2015), kde bol navrhnutý aj vzorec, dávajúci do súvislosti vzdialenosť senzorov a excentricitu elipsy. Tento prístup zaznamenal lepšie výsledky ako postupy založené na prostom priesečníku lúčov a spriemerovávaní rýchlostí v týchto priesečníkoch. Metóda dostala názov Ellipse-based spatial interpolation a skratku EBSI.

Praktická implementácia metódy rekonštrukcie obrazu spočíva v tom, že prierez kmeňa sa rozdelí na jednotlivé bunky, v ktorých sa namerané hodnoty v istom zmysle spriemerujú. V EBSI metóde pre každú bunku určíme rýchlosť ako priemer rýchlostí všetkých lúčov, v ktorých eliptickom okolí pôsobnosti sa bunka nachádza.

V ďalších prácach bola metóda EBSI ešte rozšírená Okolo každého lúča uvažujeme opäť elipsu definujúcu oblasť pôsobnosti tohto lúča (viz. Obrázok 3). Údaje sa spracovávajú dvojkolovo metódami RSEN a SISE (z anglického ray sementation by elliptical neighborhood a spatial interpolation by segmented ellipse) popísanými v Du et al (2018).

Detailný popis metód je možné nájsť v pôvodnej literatúre, avšak aj zo uvedeného zjednodušeného popisu je zrejmé, že zásadnou dielčou úlohou pri implementácii obrazovej rekonštrukcie je overenie, či bod v rovine leží vnútri elipsy či či leží vonku.

Rovnica elipsy

Z predošlej motivačnej časti vyplýva, že pre praktickú implementáciu rekonštrukcie obrazu pomocou EBSI metódy je nutné vedieť efektívne pracovať s elipsou v rôznych polohách, čo zahŕňa ľubovoľné pootočenie osí a ľubovoľné posunutie stredu elipsy. Potrebujeme efektívne zisťovať, či nejaký bod leží vnútri či vonku elipsy.

Elipsa je množina bodov v rovine, pre ktoré platí, že súčet vzdialeností bodu od dvoch ohnisiek je konštantný. Elipsu je možné určiť pomocou hlavnej a vedľajšej osi. Uvažujme elipsu s dĺžkou hlavnej poloosy \(a\) a dĺžkou vedľajšej poloosy \(b\). Rovnica elipsy so stredom v počiatku sústavy súradníc a hlavnou osou v smere osi \(x\) má v tomto prípade tvar \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1. \] Body ležiace vnútri elipsy potom spĺňajú nerovnicu \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}<1. \] My však pracujeme s elipsami vo všeobecnej polohe, ich rovnice sa síce dajú transformovať do rovnakého tvaru, ale to je pomerne pracný a pre naše účely aj zbytočný proces. Radšej než pracovať so súradnicami budeme využívať vzdialenosti bodu od hlavnej a od vedľajšej poloosy. Ak má elipsa vyššie uvedenú rovnicu, tak tieto vzdialenosti sú priamo \(x\)-ové a \(y\)-ové súradnice daného bodu.

Teda ak je \(d_1\) vzdialenosť bodu od priamky definovanej vedľajšou osou (pre stručnosť vzdialenosť od vedľajšej osi) a vzdialenosť bodu od hlavnej osi \(d_2\), potom bod leží vnútri elipsy práve vtedy, keď platí \[ \frac{d_1^2}{a^2}+\frac{d_2^2}{b^2}<1.\tag{1} \] Pre overenie či bod leží alebo neleží vnútri elipsy teda stačí určiť vzdialenosť bodu od hlavnej a od vedľajšej osi a overiť platnosť vyššie uvedenej nerovnice (1).

Dĺžka projekcie vektora a skalárny súčin

Obrázok znázorňuje hlavnú a vedľajšiu os elipsy, jednotkové vektory v smere týchto osí, spojnicu testovaného bodu so stredom elipsy a vyznačenie vzdialeností bodu od jednotlivých osí elipsy.

Pre jednoduchost uvažujme, že uhol medzi vektormi \(\vec u\) a \(\vec e_1\) je ostrý. Z definície skalárneho súčinu a z faktu, že vektor \(\vec e_1\) je jednotkovým vektorom vyplýva

\[\vec u\cdot\vec e_1 = |\vec u||\vec e_1|\cos\varphi = |\vec u| \cos\varphi = d_1.\]

Vzdialenosť od vedľajšej osi je teda možné určiť pomocou skalárneho súčinu. Kolmý priemer vektora do priamky sa nazýva projekcia a z obrázku je zrejmé, že \(d_1\) je vlastne dĺžka projekcie vektora \(\vec u\) do smeru určeného vektorom \(\vec e_1\). V prípade, že by uhol medzi vektormi \(\vec u\) a \(\vec e_1\) bol tupý, vychádza hodnota \(d_1\) záporná, čo sa však v testovacom kritériu (1) neprejaví.

Analogicky, dĺžka projekcie vektora \(\vec u\) do smeru definovaného vektorom \(\vec e_2\) je (až na prípadné znamienko, ktoré sa opäť v teste (1) neprejaví) daná vzťahom

\[d_2=\vec u\cdot \vec e_2.\]

Poznámka. Poznamenajme, že výpočet skalárneho súčinu sa vykonáva pomocou súradníc podľa vzorca

\[\vec u\cdot\vec v = u_1v_1+u_2v_2,\]

kde \(\vec u = (u_1, u_2)\) a \(\vec v=(v_1,v_2)\). Tento výpočet je možné realizovať v počítačoch veľmi rýchlo a použitím vhodných programovacích techník (vektorizácia) je možné výpočet vykonať súčasne pre tisíce bodov rádovo stokrát rýchlejšie ako použitím cyklu založeného na postupnom testovaní jednotlivých bodov.

Poznámka. Jednotkový vektor \(\vec e_1\) v smere hlavnej osi je možné určiť buď ako podiel vektora zo stredu do hlavného vrcholu a dĺžky tohto vektora, alebo pomocou uhla, ktorý zviera hlavná os s osou \(x\). Ak je tento uhol \(\alpha\), je jednotkový vektor daný vzťahom

\[\vec e_1=(\cos\alpha, \sin\alpha).\]

Jednotkový vektor v smere vedľajšej osi je na \(\vec e_1\) kolmý. Je teda možné brať napríklad

\[\vec e_2 = (-\sin\alpha, \cos\alpha).\]

Ukážka použitia

Riešenie. Jednotkový vektor so smerom hlavnej osi je \(\vec e_1=(\cos 30^\circ, \sin 30^\circ)\). Vektor \(\vec u\) je daný súradnicami bodu \(X\), t. j. \(\vec u=(1{,}6;1{,}6)\). Skalárny súčin je teda

\[d_1=\vec u\cdot \vec e_1 = 1{,}6\cdot\cos 30^\circ + 1{,}6\cdot\sin 30^\circ\doteq 2{,}186.\]

Podobne, dĺžka projekcie do smeru vedľajšej osi danej vektorom \(\vec e_2=(-\sin 30^\circ,\, \cos 30^\circ)\) je

\[d_2=\vec u\cdot \vec e_2 = -1{,}6\cdot\sin 30^\circ + 1{,}6\cdot\cos 30^\circ \doteq 0{,}586.\]

Platí

\[ \frac{d_1^2}{a^2} + \frac{d_2^2}{b^2} \doteq 0{,}683<1. \]

Bod teda leží vnútri elipsy. Situácia je na nasledujúcom obrázku.

Záver

V texte boli predstavené základné kroky, na ktorých je založená rekonštrukcia obrazu v akustickom tomografe. Jednou z dielčích úloh je overenie, či skúmaný bod leží vnútri či vonku elipsy, ktorá je vo všeobecnej polohe a je zadaná svojimi poloosami. Pre toto overenie je výhodné použiť rovnicu elipsy založenú nie na súradniciach, ale na vzdialenostiach od hlavnej a vedľajšej osi. Túto vzdialenosť je možné určiť pomocou skalárneho súčinu vektorov.

Literatúra a zdroje obrázkov

Literatúra

1. Du, X., Li, S., Li, G., Feng, H., and Chen, S. (2015). “Stress wave tomography of wood internal defects using ellipse-based spatial interpolation and velocity compensation,” BioRes. 10(3), 3948-3962. http://doi.org/10.15376/biores.10.3.3948-3962
2. Du, X.; Li, J.; Feng, H.; Chen, S. Image Reconstruction of Internal Defects in Wood Based on Segmented Propagation Rays of Stress Waves. Appl. Sci. 2018, 8, 1778. https://doi.org/10.3390/app8101778

Zdroje obrázkov

1. Projekt DYNATREE – Tree Dynamics: Understanding of Mechanical Response to Loading, https://starfos.tacr.cz/cs/projekty/LL1909.
2. Vlastné obrázky